Skip to content
opendata.studio docs

Creating a model fitting datakit

In this tutorial, we’ll explore a practical example of creating a model fitting datakit.

By the end, we’ll have created a datakit that can fit a linear or quadratic model to an x/y input dataset using scipy. We’ll add a view to graph the resulting fit curve against the data, and use relationships to handle different parameters for each model.

Creating a new datakit

First, we need to create a new datakit:

Terminal window
dk new modelfit
cd modelfit-datakit

Creating the algorithm configuration

Next, we will need to put together an algorithm configuration for our model fitting algorithm.

Open up modelfit/algorithm.json and replace its contents with the following configuration:

modelfit/algorithm.json
{
  "name": "modelfit",
  "title": "Model fitting example",
  "description": "A simple model fitting algorithm demonstrating relationships",
  "profile": "datakit-algorithm",
  "code": "algorithm.py",
  "container": "opendatastudio/python-run-base:latest",
  "signature": {
    "inputs": [
      {
        "name": "data",
        "title": "Data",
        "description": "Input data to fit to model",
        "type": "resource",
        "profile": "tabular-data-resource",
        "null": false,
        "default": {
          "resource": "data"
        }
      },
      {
        "name": "model",
        "title": "Model",
        "description": "The model to use for fitting",
        "type": "string",
        "null": false,
        "enum": [
          {
            "title": "Linear",
            "value": "linear"
          },
          {
            "title": "Quadratic",
            "value": "quadratic"
          }
        ],
        "default": {
          "value": "linear"
        }
      },
      {
        "name": "inputParams",
        "title": "Model",
        "description": "The input fit parameters",
        "type": "resource",
        "profile": "tabular-data-resource",
        "null": false,
        "default": {
          "resource": "inputParams"
        }
      }
    ],
    "outputs": [
      {
        "name": "outputParams",
        "title": "Fit",
        "description": "The optimised fit parameters",
        "type": "resource",
        "profile": "tabular-data-resource",
        "null": true,
        "default": {
          "resource": "outputParams"
        }
      },
      {
        "name": "fit",
        "title": "Fit",
        "description": "The optimised fit curve",
        "type": "resource",
        "profile": "tabular-data-resource",
        "null": true,
        "default": {
          "resource": "fit"
        }
      }
    ]
  }
}

This configuration defines three inputs: data, model and inputParams. data and inputParams are tabular data resources, defining the input data table and input parameter table respectively. model is a string that can take one of two values: “linear” or “quadratic”. This tells the algorithm which model we want to fit.

Similarly, we’ve defined two tabular resource outputs: outputParams and fit. These are the output parameter table containing optimised parameter values, and the calculated optimised fit curve.

Writing the algorithm

We want to create an algorithm that will take our input data and parameters, and fit it to the selected model. Replace the code in modelfit/algorithm.py with the following:

modelfit/algorithm.py
import pandas as pd
from typing import TypedDict
from scipy.optimize import curve_fit




class Output(TypedDict):
    outputParams: pd.DataFrame
    fit: pd.DataFrame




# Fit model functions




def linear(x, a, b):
    """Linear fit model"""
    return a * x + b




def quadratic(x, a, b, c):
    """Quadratic fit model"""
    return a * x**2 + b * x + c




# Main algorithm function




def main(data: pd.DataFrame, model: str, inputParams: pd.DataFrame) -> Output:
    """Fit a linear or quadratic model to some data"""


    params, _ = curve_fit(
        f=globals()[model],  # Call the global function named "model"
        xdata=data.index,
        ydata=data["y"],
        p0=inputParams["init"],
    )


    # Transform curve_fit output into expected output table format
    names = ["a", "b", "c"]
    table = [[name, param] for name, param in zip(names, params)]
    outputParams = pd.DataFrame(
        table,
        columns=["name", "value"],
    )


    # Calculate the optimised fit curve
    fit = data.copy(deep=True)
    fit["y"] = globals()[model](fit.index, *params)


    return {
        "outputParams": outputParams,
        "fit": fit,
    }

Let’s go through this section-by-section:

modelfit/algorithm.py
# Fit model functions




def linear(x, a, b):
    """Linear fit model"""
    return a * x + b




def quadratic(x, a, b, c):
    """Quadratic fit model"""
    return a * x**2 + b * x + c

First, we define the fit model functions. These are the functions we will be fitting to our data. They take the format expected by the scipy curve_fit function - a list of x values as the first argument, and then each individual fit parameter as a separate argument.

modelfit/algorithm.py
def main(data: pd.DataFrame, model: str, inputParams: pd.DataFrame) -> Output:
    """Fit a linear or quadratic model to some data"""


    params, _ = curve_fit(
        f=globals()[model],  # Call the global function named "model"
        xdata=data.index,
        ydata=data["y"],
        p0=inputParams["init"],
    )

Next, we define the main algorithm function, which will be executed when the algorithm runs.

Here we use the scipy curve_fit function to optimise our chosen model.

The f argument specifies the function we want to use to fit the data: in our case, it is chosen by the value of model algorithm variable which will either be linear or quadratic. This will call the relevant fit model function defined above when the algorithm is run.

xdata and ydata are simply the respective input data columns.

And p0 is an array of initial parameter guesses that are passed in via the inputParams resource.

modelfit/algorithm.py
    # Transform curve_fit output into expected output table format
    names = ["a", "b", "c"]
    table = [[name, param] for name, param in zip(names, params)]
    outputParams = pd.DataFrame(
        table,
        columns=["name", "value"],
    )

Next, we do some data munging to transform the output of curve_fit into the tabular format that our outputParams resource expects.

modelfit/algorithm.py
    # Calculate the optimised fit curve
    fit = data.copy(deep=True)
    fit["y"] = globals()[model](fit.index, *params)


    return {
        "outputParams": outputParams,
        "fit": fit,
    }

And finally, we calculate the fit curve using the parameters returned by curve_fit, and return our output data as per the outputs defined in the algorithm configuration.

Creating resources

Before we can run our new algorithm, we need to create the resources it expects as inputs and outputs: data, inputParams, outputParams and fit.

Create the resources directory:

Terminal window
mkdir modelfit/resources

And create the following resource files:

Data

modelfit/resources/data.json
{
  "name": "data",
  "title": "Data",
  "description": "Data to fit to model",
  "profile": "tabular-data-resource",
  "schema": {
    "primaryKey": "x",
    "fields": [
      {
        "name": "x",
        "title": "X",
        "unit": "",
        "type": "number"
      },
      {
        "name": "y",
        "title": "Y",
        "unit": "",
        "type": "number"
      }
    ]
  },
  "data": []
}

This configuration specifies that we can accept a two column table with the column names “x” and “y” as input.

Input parameters

modelfit/resources/inputParams.json
{
  "name": "inputParams",
  "title": "Input parameters",
  "description": "Fit parameter initial guesses",
  "profile": "tabular-data-resource",
  "schema": {
    "primaryKey": "name",
    "fields": [
      {
        "name": "name",
        "title": "Name",
        "description": "The name of the parameter",
        "type": "string"
      },
      {
        "name": "init",
        "title": "Initial value",
        "description": "The initial guess for the parameter value",
        "type": "number",
        "unit": ""
      }
    ]
  },
  "data": [
    {
      "name": "a",
      "init": 3
    },
    {
      "name": "b",
      "init": 10
    }
  ]
}

This specifies that we can accept our input parameters in a two-column table format. Our table is pre-populated with rows named “a” and “b” representing individual initial parameter guesses.

Output parameters

modelfit/resources/outputParams.json
{
  "name": "outputParams",
  "title": "Output parameters",
  "description": "Optimised parameter values",
  "profile": "tabular-data-resource",
  "schema": {
    "primaryKey": "name",
    "fields": [
      {
        "name": "name",
        "title": "Name",
        "description": "The name of the parameter",
        "type": "string"
      },
      {
        "name": "value",
        "title": "Optimised value",
        "description": "The optimised parameter value",
        "type": "number",
        "unit": ""
      }
    ]
  },
  "data": [
    {
      "name": "a",
      "value": null
    },
    {
      "name": "b",
      "value": null
    }
  ]
}

Similar to inputParams, this specifies that we expect our output parameters to be returned in a two-column table format. Our table is pre-populated with rows named “a” and “b” representing individual optimised parameter outputs.

Fit

modelfit/resources/fit.json
{
  "name": "fit",
  "title": "Fit",
  "description": "The optimised fit curve",
  "profile": "tabular-data-resource",
  "schema": {
    "primaryKey": "x",
    "fields": [
      {
        "name": "x",
        "title": "X",
        "unit": "",
        "type": "number"
      },
      {
        "name": "y",
        "title": "Y",
        "unit": "",
        "type": "number"
      }
    ]
  },
  "data": []
}

Similar to data, this specifies that we expect the calculated fit curve to be output as a two column table with the column names “x” and “y”.

Adding input data

In order to run our algorithm, we need some test data. Pase the following into data/modelfit.csv:

data/modelfit.csv
x,y
0,0.3466236167739929
1,-0.423531510762412
2,0.8388100195422679
3,2.948000020477774
4,2.45167677777786
5,5.4766419552463645
6,4.879323325885309
7,8.25876172347388
8,6.442649354518041
9,10.17816299109899
10,10.638275752972232
11,10.39655032109732
12,13.752753943890596
13,12.871660648894213
14,15.105225370942517
15,13.082135038555602
16,17.012134132693777
17,15.068090876715434
18,16.356537810690007
19,20.825401723837388

Running the algorithm

Now that we’ve created our algorithm configuration, algorithm code, and our input and output resources, we are ready to run the algorithm.

Initialise the default run:

Terminal window
dk init

Load the input data:

Terminal window
dk load data data/modelfix.csv

And execute the run:

Terminal window
dk run

Once our algorithm finishes running, we can then view our outputs:

Terminal window
dk show outputParams
dk show fit

Creating a graph visualisation

In order to be able to analyse whether our fit was a good one, we need to be able to graph the calculated fit curve.

We can create a graph visualisation by defining a view on our datakit.

First, create a views directory under the algorithm folder:

Terminal window
mkdir modelfit/views

Now we can write a view configuration for our fit graph:

"modelfit/views/fitGraph.json
{
  "name": "fitGraph",
  "specType": "matplotlib",
  "specFile": "fitGraph.py",
  "container": "opendatastudio/python-run-base:latest",
  "resources": ["data", "fit"]
}

Here we are telling our datakit that we want to use a matplotlib script, fitGraph.py, to generate this view, and we want to execute this graph script in the python-run-base container.

Now we can create our graph script:

modelfit/views/fitGraph.py
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.figure import Figure




def main(data: pd.DataFrame, fit: pd.DataFrame) -> Figure:
    plt.scatter(data.index, data["y"], label="Data", color="royalblue")
    plt.plot(fit.index, fit["y"], label="Fit", color="darkorange")
    plt.legend()


    # Return current figure
    return plt.gcf()

Now we can execute the view script and generate the graph. Run the following command:

Terminal window
dk view fitGraph

This command will execute our graph script in the python-run-base container, and then serve the resulting graph on a webpage for you to view.

In your browser, navigate to http://localhost:8988. You should see the following:

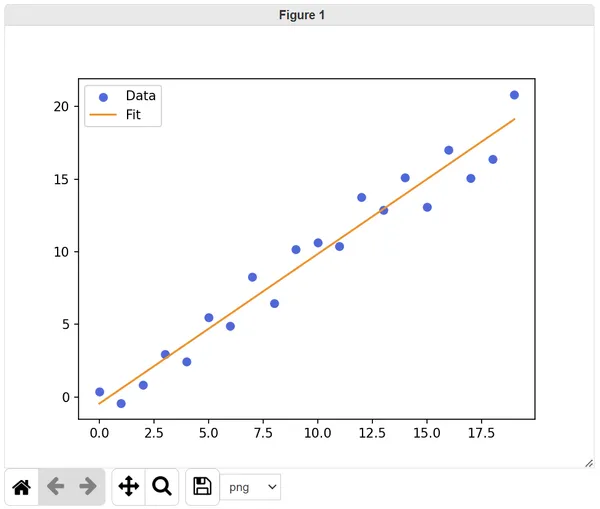
A graph of the calculated linear model fit curve

Using relationships to accept an extra parameter

Introduction to relationships

You may have noticed earlier that in our quadratic model fit function definition, we need an extra input parameter - c. However, this parameter isn’t specified anywhere in our algorithm configuration or parameter resources.

In order to fit to a quadratic model, we need a way to dynamically add an extra parameter whenever the value of the model algorithm variable is set to quadratic.

We can do this using relationships. Relationships in a datakit describe relationships between variables. Whenever a variable changes, the CLI checks if there are any relationships that apply to that variable value, and if so updates any associated variables to the required values.

Relationships are defined in the algorithm directory under modelfit/relationships.json.

Creating relationships

In order to add an extra parameter whenever the value of model is set to quadratic, we need to write two relationship rules. Create the modelfit/relationships.json file and write the following rules:

modelfit/relationships.json
{
  "name": "relationships",
  "title": "Relationships",
  "descriptions": "Relationship rules for model fit algorithm inputs and outputs",
  "profile": "datakit-relationships",
  "algorithm": "modelfit",
  "relationships": [
    {
      "source": "model",
      "rules": [
        {
          "description": "Linear model parameter defaults",
          "type": "value",
          "values": ["linear"],
          "targets": [
            {
              "name": "inputParams",
              "type": "resource",
              "data": [
                {
                  "name": "a",
                  "init": 3
                },
                {
                  "name": "b",
                  "init": 10
                }
              ]
            },
            {
              "name": "outputParams",
              "type": "resource",
              "data": [
                {
                  "name": "a",
                  "value": null
                },
                {
                  "name": "b",
                  "value": null
                }
              ]
            }
          ]
        },
        {
          "description": "Quadratic model parameter defaults",
          "type": "value",
          "values": ["quadratic"],
          "targets": [
            {
              "name": "inputParams",
              "type": "resource",
              "data": [
                {
                  "name": "a",
                  "init": 3
                },
                {
                  "name": "b",
                  "init": 10
                },
                {
                  "name": "c",
                  "init": 5
                }
              ]
            },
            {
              "name": "outputParams",
              "type": "resource",
              "data": [
                {
                  "name": "a",
                  "value": null
                },
                {
                  "name": "b",
                  "value": null
                },
                {
                  "name": "c",
                  "value": null
                }
              ]
            }
          ]
        }
      ]
    }
  ]
}

Breaking down the relationship configuration

In this relationship configuration, we are specifying that our source variable is model. This means that we want to execute a set of rules whenever this variable changes.

modelfit/relationships.json
  ...
  "relationships": [
    {
      "source": "model",
      "rules": [
        ...
      ]
    }
  ]

Each source variable can have any number of rules associated with it.

Each individual rule applies to a set of values of the source variable specified in values. Whenever the source variable matches one of these values, the associated rule will be executed.

modelfit/relationships.json
  ...
  "relationships": [
    {
      "source": "model",
      "rules": [
        {
          ...
          "values": [
            "linear"
          ],
          "targets": [
            ...
          ]
        }
      ]
    }
  ]

We can specify which associated variables we want to update when a rule is triggered in targets. For example, below we are targeting the resource inputParams. Whenever our source variable model is updated to the value linear, we set the inputParams resource data to the specified values.

modelfit/relationships.json
{
  ...
  "relationships": [
    {
      "source": "model",
      "rules": [
        {
          "values": [
            "linear"
          ],
          "targets": [
            {
              "name": "inputParams",
              "type": "resource",
              "data": [
                {
                  "name": "a",
                  "init": 3
                },
                {
                  "name": "b",
                  "init": 10
                }
              ]
            }
  ...

Putting it all together

Putting it all together, the above relationship configuration is doing the following:

  • Whenever the model value is updated to linear, it updates the input and output parameter resources to contain two variables - a and b.
  • Whenever the model value is updated to quadratic, it updates the input and output parameter resources to contain three variables - a, b and c.

In this way, we can dynamically handle a different number of parameters depending on the fit model chosen.

Running the algorithm again

Let’s test this out by running the algorithm again. Check the current parameter values:

Terminal window
dk show inputParams
╭────────┬────────╮
│ name   │   init │
├────────┼────────┤
│ a      │      3 │
├────────┼────────┤
│ b      │     10 │
╰────────┴────────╯

Now let’s set the model to quadratic:

Terminal window
dk set model quadratic

And check the parameter values again:

Terminal window
dk show inputParams

You should see the following:

╭────────┬────────╮
│ name   │   init │
├────────┼────────┤
│ a      │      3 │
├────────┼────────┤
│ b      │     10 │
├────────┼────────┤
│ c      │      5 │
╰────────┴────────╯

As you can see, an extra parameter called c has been added.

Now we can run the algorithm and view the optimised parameters:

Terminal window
dk run
dk show outputParams
╭────────┬─────────────╮
│ name   │       value │
├────────┼─────────────┤
│ a      │ -0.00663661 │
├────────┼─────────────┤
│ b      │  1.15614    │
├────────┼─────────────┤
│ c      │ -0.838431   │
╰────────┴─────────────╯

And have a look at our resulting fit curve:

Terminal window
dk view fitGraph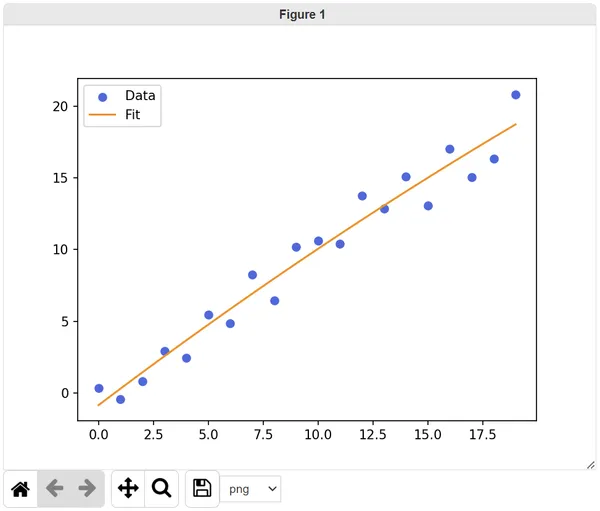
A graph of the calculated quadratic model fit curve

Congratulations, you’ve written and executed your own model fitting datakit.